Damage: Power, Precision, and Golden Ratios
Overview
This is an analysis of damage output that considers the relative effectiveness of power and precision. I will describe in detail how I performed the analysis, what assumptions I used, and how to interpret the data.
Some of the findings presented will be obvious, and some may not be. But the important thing here is that they are all directly backed by the numbers. If you see any errors, let me know.
Basics and Assumptions
In order to be able to make claims about damage output, I am exploiting the proportional relationship between damage and power. This does not mean that power is the only thing that factors into damage output; this means that I’ve held all other factors that exist outside of a character’s stats (target’s armor, skill coefficient, weapon damage) static and utilized standardized percentage differences in calculations. The only three components of damage output in question are power, critical strike chance (governed by precision), and critical strike damage.
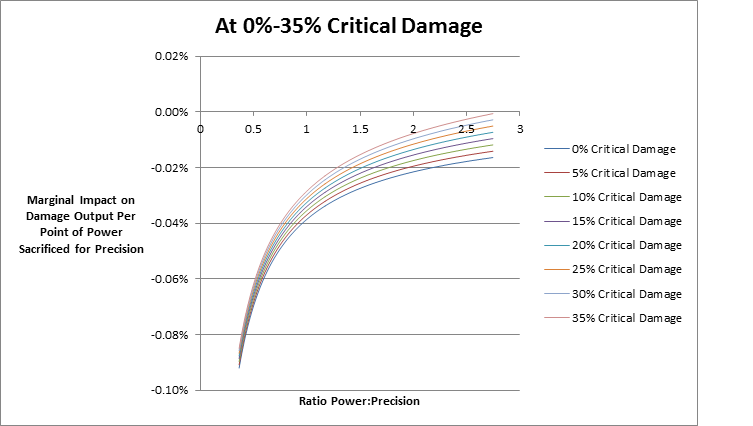
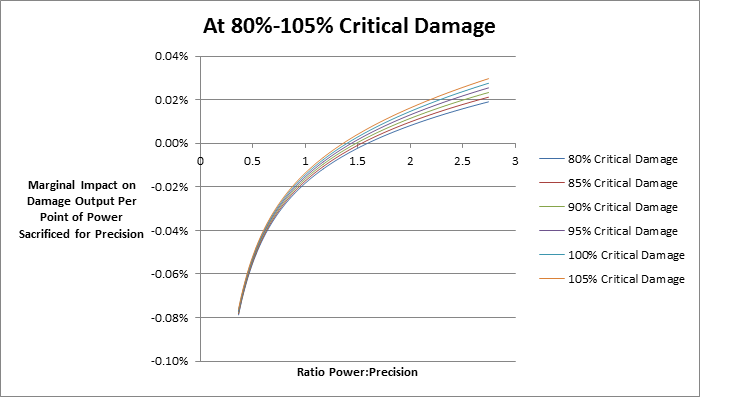
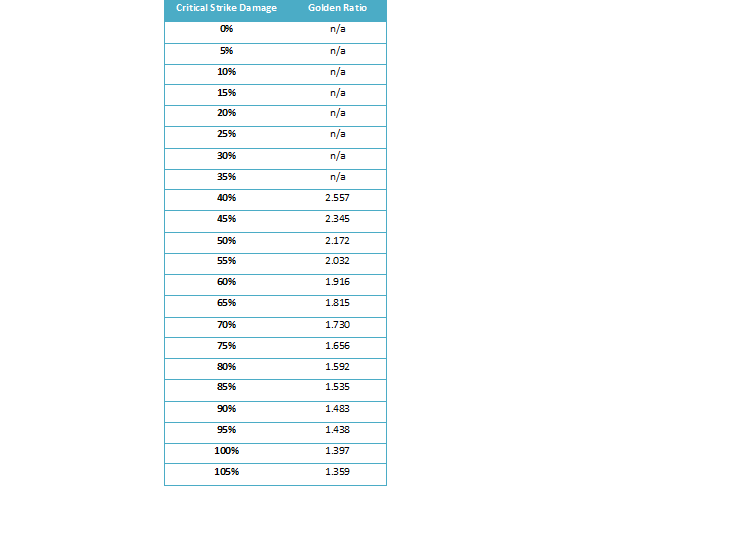
As a caveat, 3-variable functions are extremely complex. In the interest of avoiding the calculus (for multiple reasons) I opted to focus on the relationship between power and precision, and then place this relationship in a series of discrete contexts that reference critical damage. This methodology is necessarily less precise, but it is much simpler to execute, display, and explain.
Here are some assumptions to keep in mind:
1. This analysis only accounts for a character’s permanent power and precision (base stats + hard/invariable stat increases from gear/upgrades), and does not apply to special bonuses from sigils, traits, runes, boons, etc. It strictly applies to the direct damage dealt by skills.
2. I operate from the perspective of damage over the long-run. This means that if a character has 40% critical strike chance, said character will crit on exactly 40% of attacks, ad infinitum. This also means that any damage governed by a weapon’s damage spread will revert to the mean.
3. In order to reflect relative value, I had to set a limit to the sum of a character’s power and precision. While this limit is arbitrary, I tried to account for the widest realistic range without including any instance of impossibility (such as a critical chance of over 100%).
4. Whenever I refer to “critical damage,” I am referring to the critical damage bonus seen in your stats. For example, 35% critical damage means that your critical strikes will do 185% (150% + 35%) of your base damage. Mathematically, 185% means a multiplier of 1.85.
5. Everything in this analysis assumes that the character is level 80. I do not know if character stat progression is linear, so I cannot say if it is applicable to characters under level 80. If progression is linear, then theoretically it would apply.
6. Many builds depend on critical hits to proc various things, but this does not always apply to direct damage and cannot always be strictly quantified. Therefore, this aspect of the game is not reflected here.
How Direct Damage Works
In simplifying the mechanics of damage output to the greatest degree, we are left with the 3 variables of power, critical strike chance, and critical strike damage. Power is the fundamental component here; it factors in to damage output regardless of whether or not a critical strike was performed. As mentioned before, although base damage is affected by things like the target’s armor level, it is directly proportional to power. We can use this to our advantage by ignoring those other elements, which only serve as a fluctuating coefficient to power (as a variable).
We know how precision relates to critical strike chance. At level 80, every 21 points of precision (above 916) increases critical strike chance by 1% (above the base 4%). This relationship is very easily made into a function. We also know that critical strike damage applies during a critical strike and further increases damage past 150% of base damage.
Pulling all of this information together, we can arrive at the following:
Damage = [Power * (1.50 + Critical Damage) * Critical Chance] + [Power * (1 – Critical Chance)]
What this states is that damage is a weighted average of the damage done on critical strikes and the damage done on non-critical strikes, weighted by the chance of each occurring (critical strike chance). The output of the above equation will not reflect actual damage (because there are factors that are not considered) but it will reflect a referential damage LEVEL that we can make claims about upon changing the inputs. This damage level directly relates to the actual amount of damage that would be done.