Guild Wars 2

Justin said in another thread:

“I can mostly explain the first match (a blowout against top players). They had a very low rated player on their team, which skewed the average much closer to your team.”

Below is an example to think about. I’d like to hear your thoughts on it.

How should this be predicted by the Match Prediction?

Team 1:
MMR 2400 On TS, expert rotation knowledge
MMR 2200 On TS, expert rotation knowledge
MMR 2300 On TS, expert rotation knowledge
MMR 550
MMR 500

Average: 1590
============

Team 2:
MMR 1490
MMR 1600
MMR 1450 On TS , low rotation knowledge
MMR 1550 On TS , low rotation knowledge
MMR 1500

Average: 1518

Knowing the complexities of the game, can this situation be accurately represented by average numbers?

I’d like to hear the thoughts of people who know the game well about how this match would actually play out in reality, vs the math of averages.

What?

Team 1 would win and carry hard

dont forget to mention the low mmrs on team 1 are only low because they are deserters and before some tuesday deserting affected your mmr.

this is a classic case of match manipulation, which will no longer be possible since deserting no longer affects mmr.

insanemaniac.2456:

dont forget to mention the low mmrs on team 1 are only low because they are deserters and before some tuesday deserting affected your mmr.

this is a classic case of match manipulation, which will no longer be possible since deserting no longer affects mmr.

Other likely explanations for low MMR is low experience and no skill yet. And that they joined ranked too early.

Justin,

It’s a tough, thankless challenge you guys have.

methinks math should not allow 1 team to have both extremely high and extremely low MMR players.

methinks there needs to be a maximum difference in skill ranges within a match

methinks no match should ever have both pro and noob players in it

edit: unless they queue together of course. which makes me think… maybe system should use median for parties and mean for pugs. in a 3+1+1 it would be (the median of the 3 × 3 + the MMRs of the 2 pugs) / 5

Laserbolt.6731:

insanemaniac.2456:

dont forget to mention the low mmrs on team 1 are only low because they are deserters and before some tuesday deserting affected your mmr.

this is a classic case of match manipulation, which will no longer be possible since deserting no longer affects mmr.

Other likely explanations for low MMR is low experience and no skill yet. And that they joined ranked too early.

yes but in this instance youre incompletely quoting justin to mislead your readers.

Justin ODell.9517:

Solstice.1097:

i just played 5 pugs vs a premade that included toker nos supcutie and 2 others

and the next game i won by ~350+ points

i have generally not had very long queues

maybe it shouldnt resort to the extremes so quickly.

I can mostly explain the first match. They had a very low rated player on their team, which skewed the average much closer to your team.

I don’t think it was intentional though, as the low rated player had a lot of desertions that probably explain why they were so low.

I’m wondering if we need to do a blanket ratings reset for anyone with a significant number of desertions.

I don’t know the math anet use but I think match making has improved even though I was clobbered with like a 10 match losing steak in the first 2 days. It has gotten better because I almost never get matched against noobs anymore, I have to work for 90% of my wins.
It’s pretty easy to say if you have a team of 3 you bump their total mmr by 25% to calculate the avg mmr of the team. I think anet is doing their best to get good matches. It would be better if the scoreboard at the end of the match showed your %chance at wining that match according to MMR.

Yet it’s the math of finding a match in a complex situation that drives my post. We can still discuss that. My example did not talk about desertions and “fake MMRs” that are artificially low.

So desertions should not end the discussion.

Justin ODell.9517:

Solstice.1097:

methinks math should not allow 1 team to have both extremely high and extremely low MMR players.

Well, Laserbolt.6731’s example is pretty extreme. The matchmaker shouldn’t ever produce the example in this thread with all solos.

The reason for the original example (in another) thread was because it was a pre-made team that contained 4 higher MMR players, and 1 player with an artificially low MMR (due to desertions).

Is getting Solo and Team Que back still an option? You guys are trying your hardest to find the perfect balance but man, a lot of us can see the benefits of the old system compared to the new one.
Teams will get their close to even match-ups and solos won’t complain about pre-mades (just that their teams suck or some such).

As the saying goes, you only know what you’ve got until it’s gone.

To be honest Laserbolt, are you really sure team 1 would win? A 3-man team can only carry so much: if the two new players keep dying to Svanir, staying in lost fights or afking on the home node, team 2 could very well win. But like Justin, I’d like to believe that very low and very high MMR can’t be teamed like this, if they don’t play on New Year’s Eve at 11pm.

Sorel, I don’t know. But being expert at rotating and communicating is huge against an uncoordinated team.

Laserbolt.6731:

Justin said in another thread:

“I can mostly explain the first match (a blowout against top players). They had a very low rated player on their team, which skewed the average much closer to your team.”

Below is an example to think about. I’d like to hear your thoughts on it.

How should this be predicted by the Match Prediction? By average MMR and team size?

Team 1:
MMR 2400 On TS, expert rotation knowledge
MMR 2200 On TS, expert rotation knowledge
MMR 2300 On TS, expert rotation knowledge
MMR 550
MMR 500

Average: 1590
============

Team 2:
MMR 1490
MMR 1600
MMR 1450 On TS , low rotation knowledge
MMR 1550 On TS , low rotation knowledge
MMR 1500

Average: 1518

Knowing the complexities of the game, can this situation be accurately represented by average numbers?

I’d like to hear the thoughts of people who know the game well about how this match would actually play out in reality, vs the math of averages.

Is the problem that the current algorithm consider this a fair (50/50 odds) match and the consensus is that team A will always win?

How about squaring the individual ratings, averaging these and then taking the square root of the average?

Team A = 1813
Team B = 1519

This would weigh better players more. I’m not sure this is a wise solution but I think this could work mathematically to implement it

Dixo.3876:

Is the problem that the current algorithm consider this a fair (50/50 odds) match and the consensus is that team A will always win?

How about squaring the individual ratings, averaging these and then taking the square root of the average?

Team A = 1813
Team B = 1519

This would weigh better players more. I’m not sure this is a wise solution but I think this could work mathematically to implement it

I like the maths behind this idea. Yes, if we admit that it’s more difficult to win when the variance of the MMR is bigger, this would be a nice implementation. But is it really? In this example, we know who’s on TS. But if no one is? Then a team were everyone plays decently could very well win against a team with very good and very bad players. In a team game, it takes one bad apple to ruin the batch. I personally prefer seeing very bad and very good players against me in a match: I just have to focus on the good players, and know that the bad players will always lose their 1v1 pretty quickly.

aside from the obvious “matchmaking shouldnt ever do this naturally”, i guess premades with X high rated + Y nubs are a valid concern.

Sorel.4870:

To be honest Laserbolt, are you really sure team 1 would win? A 3-man team can only carry so much: if the two new players keep dying to Svanir, staying in lost fights or afking on the home node, team 2 could very well win. But like Justin, I’d like to believe that very low and very high MMR can’t be teamed like this, if they don’t play on New Year’s Eve at 11pm.

how hard can they carry though? is 3 2500s & nubs enough to reliably beat 5 2000s? 5 2100s? 5 2200s?

perhaps you could clamp the average to be within say 300 of the highest players (since a difference of about 200 produces wins like 90-95% of the time). something like that would be fairly inelegant because you would need a bunch of if-then cases to accommodate various premade sizes.

like say a 500 and a 2500 queue together — the mean would be 1500 but of course the 2500 should never be matched so far outside of his rating, so clamp the mean to 2200. the minimum rated player that the 2500 could queue with without artificially forcing the system to start accounting for the players ridiculous tendency to faceroll in poor matches no matter what would be a 1900.

#showertimeisthinkingtime

Sorel.4870:

Dixo.3876:

Is the problem that the current algorithm consider this a fair (50/50 odds) match and the consensus is that team A will always win?

How about squaring the individual ratings, averaging these and then taking the square root of the average?

Team A = 1813
Team B = 1519

This would weigh better players more. I’m not sure this is a wise solution but I think this could work mathematically to implement it

I like the maths behind this idea. Yes, if we admit that it’s more difficult to win when the variance of the MMR is bigger, this would be a nice implementation. But is it really? In this example, we know who’s on TS. But if no one is? Then a team were everyone plays decently could very well win against a team with very good and very bad players. In a team game, it takes one bad apple to ruin the batch. I personally prefer seeing very bad and very good players against me in a match: I just have to focus on the good players, and know that the bad players will always lose their 1v1 pretty quickly.

Yeah it’s totally up in the air in my mind which team would win. It hinges on what the MMR rating correlate to. I’ll buy that three elite players could carry two bass against five average players. I don’t think three great players could carry two terrible players against five less than geat players.

Are there options in place to try to match the team average MMR and the variance of the team MMR?

Sorel.4870:

To be honest Laserbolt, are you really sure team 1 would win? A 3-man team can only carry so much: if the two new players keep dying to Svanir, staying in lost fights or afking on the home node, team 2 could very well win. But like Justin, I’d like to believe that very low and very high MMR can’t be teamed like this, if they don’t play on New Year’s Eve at 11pm.

I agree, Team 2 is more equilibrated in skill, TS trio in Team 1 needs to carry really hard to compensate (probably) a bad game of other duo.

This is in general, maybe the duo would play 2 turrets engi, so it’s not really easy to establish only with math, who will win and odds (i always think profs and role have an high impact on winning chance).

In general I think Matchmaking shouldn’t match Team1 in this way, there is too much difference in rating between trio and duo and there isn’t the same situation in the other team.

You guys are making good points. Theoretically, Anet could use the data from the test season to find all the balanced matches were the variance of the MMR between the two was sensibly different, and see which team tends to win. If you’re right, the team with the lowest variance would statistically win. But I have no idea how much time that would cost, and I doubt they do it in the near future, especially when the “bring soloq back” crowd monopolizes the debate on match making.

Sorel.4870:

You guys are making good points. Theoretically, Anet could use the data from the test season to find all the balanced matches were the variance of the MMR between the two was sensibly different, and see which team tends to win. If you’re right, the team with the lowest variance would statistically win.

Good idea. Sounds like the kind of thing Justin tries to do with his simulations.

This example feels to me like Team A has a predicted win likelihood of 85%. Team B at 15%.

Which means Team B has to at least score 200 points, or they all get penalized on the leaderboard.

Justin ODell.9517:

Adding the math for a few of the suggestions I’ve seen.

Geometric Mean = (a*b*c*d*e)^(1/5)
Team 1: 1273
Team 2: 1517

Center = (min(a,b,c,d,e)+max(a,b,c,d,e))/2
Team 1: 1450
Team 2: 1525

Median = c
Team 1: 2200
Team 2: 1500

Before saying one is superior, try finding contradicting examples.

For example, I don’t like median for instances like this:
(2500, 2500, 1500, 1500, 1500) vs (1500, 1500, 1500, 1500, 1500)
Both have a median of 1500, but clearly team 1 would have the advantage.

Have you thought about using a (molecular) weight versus (molecular) number average like in polymer science? You could use the equivalent of the polydispersity for the system to see how the team values are skewed to the upper or lower mmr values.

Simplistic overview of weight versus number average :
http://www.pslc.ws/macrog/weight.htm

Polydispersity Overview:

http://en.m.wikipedia.org/wiki/Dispersity

Maugetarr.6823:

Justin ODell.9517:

Adding the math for a few of the suggestions I’ve seen.

Geometric Mean = (a*b*c*d*e)^(1/5)
Team 1: 1273
Team 2: 1517

Center = (min(a,b,c,d,e)+max(a,b,c,d,e))/2
Team 1: 1450
Team 2: 1525

Median = c
Team 1: 2200
Team 2: 1500

Before saying one is superior, try finding contradicting examples.

For example, I don’t like median for instances like this:
(2500, 2500, 1500, 1500, 1500) vs (1500, 1500, 1500, 1500, 1500)
Both have a median of 1500, but clearly team 1 would have the advantage.

Have you thought about using a (molecular) weight versus (molecular) number average like in polymer science? You could use the equivalent of the polydispersity for the system to see how the team values are skewed to the upper or lower mmr values.

Simplistic overview of weight versus number average :
http://www.pslc.ws/macrog/weight.htm

Polydispersity Overview:

http://en.m.wikipedia.org/wiki/Dispersity

This is the kind of useful and interesting discussion I was hoping to prompt with my post.

All of the answers have been good.

Laserbolt.6731:

Maugetarr.6823:

Justin ODell.9517:

Adding the math for a few of the suggestions I’ve seen.

Geometric Mean = (a*b*c*d*e)^(1/5)
Team 1: 1273
Team 2: 1517

Center = (min(a,b,c,d,e)+max(a,b,c,d,e))/2
Team 1: 1450
Team 2: 1525

Median = c
Team 1: 2200
Team 2: 1500

Before saying one is superior, try finding contradicting examples.

For example, I don’t like median for instances like this:
(2500, 2500, 1500, 1500, 1500) vs (1500, 1500, 1500, 1500, 1500)
Both have a median of 1500, but clearly team 1 would have the advantage.

Have you thought about using a (molecular) weight versus (molecular) number average like in polymer science? You could use the equivalent of the polydispersity for the system to see how the team values are skewed to the upper or lower mmr values.

Simplistic overview of weight versus number average :
http://www.pslc.ws/macrog/weight.htm

Polydispersity Overview:

http://en.m.wikipedia.org/wiki/Dispersity

This is the kind of useful and interesting discussion I was hoping to prompt with my post.

All of the answers have been good.

I didn’t run the numbers before, but that first team has a weight average of 2066, while the other team has a weight average of 1518. This produces a PDI of 1.3 and 1 respectively, showing that even though they have the same number average, the first is being lowered by having 2 low mmr players.

Edit: (I got to a computer instead of my phone)

So the way you would run the numbers is first by taking the sum of the mmr of each team.

For team 1 it would be 7950 and team 2 it would be 7590.

Then you would do the weight calculation for each player

Team 1:

2400*(2400/7950)=724
2200*(2200/7950)=608
2300*(2300/7950)=665
550*(550/7950)=38
500*(500/7950)=31

Weight average is then 724+608+665+38+31=2066 (Mw)

Team 2:
1490*(1490/7590)=292
1600*(1600/7590)=337
1450*(1450/7590)=277
1550*(1550/7590)=316
1500*(1500/7590)=296

292+337+277+316+296=1518 (Mw)

These weight averages may be more useful in showing whether teams should be matched or not.

PDI (polydispersity index)=Mw/Mn

Team 1: 2066/1590=1.3
Team 2:1518/1518=1

This just gives a quick reference to how much deviation there is in a team since the Mw is more sensitive to larger numbers.

Justin ODell.9517:

Maugetarr.6823:

I didn’t run the numbers before, but that first team has a weight average of 2066, while the other team has a weight average of 1518. This produces a PDI of 1.3 and 1 respectively, showing that even though they have the same number average, the first is being lowered by having 2 low mmr players.

OK, I think I understand the concept.

I think what you’re suggesting is using the mass average molecular mass formula.
http://en.wikipedia.org/wiki/Molar_mass_distribution#Mass_average_molar_mass

MAMM = (a^2+b^2+c^2+d^2+e^2) / (a+b+c+d+e)
Team 1: 2068
Team 2: 1520

I’m not sure how we would incorporate the PDI.

PDI is probably less useful than the weight average in this case. I wanted to be complete in my original suggestion though. It may only be useful in spot checking teams to see whether or not they are all close to the same mmr.

What would win here is IQ+Real-Time communication.

Justin ODell.9517:

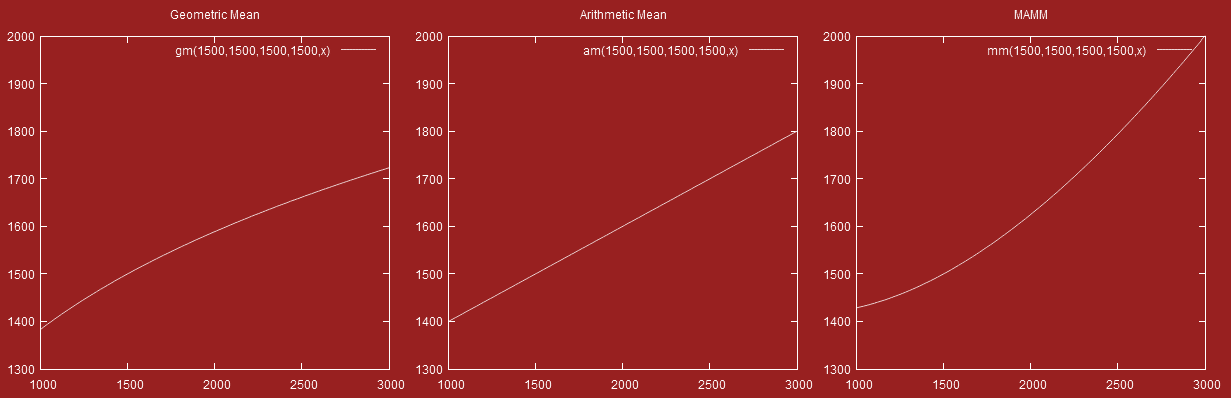
I threw together these three plots of the three most interesting ways of getting the mean of a team. The geometric mean, the (regular) arithmetic mean, and the mass average.

Y is the adjusted mean of the team, X is the 5th member on a range from 1000 to 3000.

Hopefully this gives you a better idea how each type works.

That’s an interesting way to display the differences. At first I thought the MAMM was dragging the team up too much before realizing the scales on the y and x axis were slightly different to emphasize the curves of the lines. It’s cool that the geometric mean has a little more volitility when all of players are around the same skill levels while the MAMM has more volitility in the higher differences.

Could you maybe apply the geometric one to people queuing solo to limit their highest value while applying the MAMM to premades to account for the communication between higher and lower mmr people in the premade?

Justin ODell.9517:

Maugetarr.6823:

That’s an interesting way to display the differences. At first I thought the MAMM was dragging the team up too much before realizing the scales on the y and x axis were slightly different to emphasize the curves of the lines. It’s cool that the geometric mean has a little more volitility when all of players are around the same skill levels while the MAMM has more volitility in the higher differences.

Could you maybe apply the geometric one to people queuing solo to limit their highest value while applying the MAMM to premades to account for the communication between higher and lower mmr people in the premade?

They shouldn’t be at different scales. Here is one with them overlayed.

What I meant about the scales is that the Y axis had a difference of 700 while the X axis had a difference of 2000. The overlay is a nice presentation.

Question on the score calculation. If I’m reading this right from the wiki, it adjust the score of a roster based on the absolute value of the difference in the lower bound of the roster and team ratings (not sure why it doesn’t use average, but whatever). Then it adjusts the score based on the team size, with larger teams scoring higher and a special bonus for full teams.

So here’s two scenarios using just rating and team size (assuming all else equal):

1. Lower rated partial team and average rated solo player. They end up having roughly equal scores and roughly equal chance of being picked for addition to the team.
2. higher rated partial team and lower rated solo player. They have the same absolute difference in rating, but the partial team has less penalty for size, making them a much better choice.

Scenario #2 seems counter-intuitive. A partial team of better players should somewhat easily defeat a team of solo players of equal rating. I would expect that roster size would be used as a modifier to roster rating (organization improves performance) and then that combined factor weighted.

I hope I didn’t mis-read the pseudo code.

Won’t a league system alleviate these issues? If you can only play with and against people in your league (around the same MMR scale), the only thing that will matter is how the placement and promotion matches tie into the system.

However, I still don’t see how a league system will work decently enough with the current solo/team queue mix.

Some questions from a non-math-freak:
1.) The examples at the start of this topic are very extreme. Since those should never happen in the live environment, are the different calculation methods (geometric mean; arithmetic mean; mamm) really that important?

Isn’t it more important to focus on the rating difference between the individual team member? F.e. The players in a single match are only ranked between 1500 and 1600?

How many games in percentage are currently happening, where you predict that one team will win with a 60% chance, how many with a 80% chance?
You already told us, that those predictions seems to be fairly accurate, and therefore the mmr system itself seems to work, but I’m still curious how many of those games are happening, since those are the imbalanced games.

2.) How big is the advantage of a premade team? I cannot answer this question.
If a 500 player joins a team, he will still be a rally bot, and he will mostly not profit from using voice communication. On the other hand, a 2000 solo player will most likely have expert rotation knowledge and map awareness, that he will know when the opponents respawn, and on which point he can most likely help out the most.
Therefore it is ideally to only let a premades of the same size fight against premades of the same size.

3.) How would the extreme starting example really play out? The rating difference is abysmal. For me it seems that team 1 will fight 3vs5 with the additional disadvantage of having two rally bots.

@Teutos.8620
1. Rosters (the group you queue with) expand their rating match range over time. When a roster reaches 4 minutes in queue, they’re being considered at ±500 of the roster rating. So you have a much larger range of possible ratings. In addition, you have to consider a pre-made group which can have extremes.
2. If you have a pre-made with a single player of significantly lower rating, you ask them to just stay back from the fight or put them in a role where they’re less likely to be a rally bot. Since it’s a pre-made, they’ll likely listen.

Exedore.6320:

1. Rosters (the group you queue with) expand their rating match range over time. When a roster reaches 4 minutes in queue, they’re being considered at ±500 of the roster rating. So you have a much larger range of possible ratings. In addition, you have to consider a pre-made group which can have extremes.

I know, that this is currently the case, but I strongly disagree with this procedure.
In my personal opinion players with a big rating difference should NEVER fight with / against each other.

In another post they talked about a 5% win chance for one side. This will just lead to a match nobody is happy with.

I agree, that the rating difference between the two teams can increase over time, but a match where one side ends up with 80%+ win chance should never happen, no matter how long they have already been in queue.

2. If you have a pre-made with a single player of significantly lower rating, you ask them to just stay back from the fight or put them in a role where they’re less likely to be a rally bot. Since it’s a pre-made, they’ll likely listen.

From my personal experience this will not happen, they will either end up being a burden in the team fight, or you have to fight outnumbered. => Back to 1.) the rating difference between the individual players must not be too high.

I think another problem is to assign the correct rating value at every player. Many times rating isn’t really accurate about player skill, it would be interesting to not change rating completely but adjust it with other interactions.

For example with a Personal score rework (not how it works now) to better analize the single performance and with a mvp system (only in a positive way).

Ex. rating = 70-80% how it works now +20-30% mvp + Personal score rework.